МОДЕЛИ ВОСПРОИЗВОДСТВА НАСЕЛЕНИЯ

МОДЕЛИ ВОСПРОИЗВОДСТВА НАСЕЛЕНИЯ, описывают процесс возобновления поколений; класс моделей демографических. Устанавливают связь между числ. и возрастной структурой населения, с одной стороны, и режимом рождаемости и порядком вымирания - с другой; при этом, как правило, предполагается, что нас. закрытое, т. е. миграция отсутствует. Имеются также М. в. п., учитывающие влияние на динамику нас. миграц. процессов, т. н. М в. н. с учётом миграции.

М. в. н. относятся к детерминистским макромоделям; могут быть непрерывными и дискретными. В первых время и возраст меняются непрерывно, исторически они появились раньше и служат гл. обр. для аналитич. целей. Вторые распространились с сер. 20 в., время и возраст в них изменяются с определ. шагом (обычно годовым интервалом), применяются как для практич. расчётов, так и (в меньшей степени) для анализа общих закономерностей динамики нас.

Эндогенными переменными М. в. н. служат функции и параметры, характеризующие числ. и состав нас. в нек-ром интервале времени от t₀ до t₁ или в определ. точках этого интервала. Экзогенные переменные - система количеств, характеристик рождаемости и смертности, напр. функция дожития l(х) и функция рождаемости f(x) в данном интервале от t₀ до t₁. К экзогенным переменным относятся также характеристики числ. и состава нас. в нач. момент t₀, т. н. граничные условия модели, а также характеристики миграции.

Область применения М. в. н.: 1) анализ взаимосвязей и зависимостей отд. составляющих режима воспроизводства населения и получение обобщающих характеристик воспроиз-ва нас.; 2) перспективные, ретроспективные и др. демографич. расчеты; 3) восстановление недостающих данных в условиях неудовлетворит. демографич. статистики.

Простейшие М. в. п.- модели роста - рассматривают нас. без к.-л. демографич. характеристик (первоначальный вариант модели экспоненциального населения, логистическое население и т. д.). Исходные гипотезы в них задаются без возрастной дифференциации рождаемости и смертности - в виде общих показателей прироста нас., напр. коэффициент естественного прироста населения.

К моделям, учитывающим возрастную интенсивность демографич. процессов, относятся интегральное уравнение воспроиз-ва нас. (непрерывная модель); матричные М. в. н., к к-рым принадлежит и метод передвижки по возрастам, теоретич. население, отражающее осн. закономерности воспроиз-ва нас., характерные для отд. демографич. периодов.

Большинство М. в. п. рассматривает нас. одного пола, гл. обр. женское. При необходимости данные о лицах противоположного пола рассчитываются дополнительно исходя из постоянства соотношения полов при рождении. Попытки независимого исчисления для каждого пола ведут к противоречию ('конфликту') между мужскими и женскими мерами воспроиз-ва. Противоречие состоит в том, что осн. меры воспроиз-ва нас. в нек-рый момент времени (напр., нетто-коэффи-циент воспроизводства населения), исчисленные независимо для мужчин и женщин, могут существенно различаться в силу диспропорции в соотношении численностей полов. Попытка принять мужские и женские показатели воспроиз-ва постоянными ведёт к тому, что числа рождений, рассчитанные на основе мужских показателей (у мужчин) и женских показателей (у женщин), оказываются существенно неравными, а соотношение полов при рождении со временем становится нереальным, существенно отличным от когда-либо наблюдавшихся (см. Соотношение численностей полов).

В основе М. в. н. лежат естеств. соотношения между числ. разл. групп в нас. в нек-рый момент времени. 1) Число лиц в возрасте х в момент t равно числу родившихся х лет назад, т. е. в момент t - х, умноженному на вероятность дожития до возраста х. 2) Совокупность х-летних в момент t за время τ перейдёт в возрастную группу х + τ, а их числ. уменьшится в число раз, равное вероятности дожития от возраста х до возраста х + τ. 3) Число родившихся в нек-рый момент t равно сумме чисел родившихся у женщин каждого возраста. Последняя величина равна числ. женщин данного возраста, умноженной на вероятность рождения ребёнка в этом возрасте. Формальная непрерывная запись посылок (1) и (3) даёт интегральное уравнение воспроиз-ва нас. в однородной форме; (1), (2) и (3) - то же в неоднородной форме. При дискретном представлении условий (2) и (3) получают модель передвижки по возрастам - матричную модель воспроиз-ва нас. В общем виде, если шаг модели принят равным 1 году, модель применительно к женскому нас. записывается:

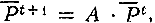
где 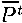- столбец возрастных числ. нас. на начало года t:

x - возраст, а

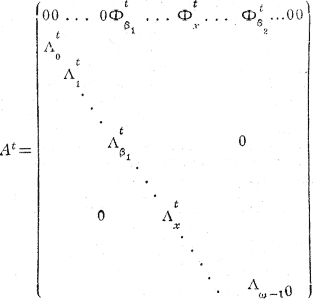
где β₁, β₂ - возрастные границы репродуктивного периода; 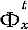- вероятность рождения девочек у женщин в возрасте х в течение календарного года t; 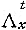- коэфф. дожития (см. Таблицы смертности), вероятность дожития для лица в возрасте х от начала года до начала следующего года. Очевидно, что 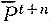= A^t+n-1 ... A_t .

Если режим воспроиз-ва неизменен, то 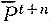= Aⁿ,

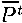где (А)ⁿ - n-я степень матрицы.

Матем. анализ М. в. н. позволяет доказать эмпирически установленные особенности воспроиз-ва нас., напр. эргодичности свойство, оценить степень инерционности роста нас. (см. Потенциал прироста населения).

При построении М. в. н. используются данные за определ. период времени, значения функций демометрических, рассчитанные для гипотетич. поколения, к-рые в силу объективных причин (см. Поперечный анализ) могут существенно отличаться от соответств. функций для реальных поколений. Так, на показатели рождаемости женского гипотетич. поколения оказывают влияние брачный состав нас., распределение женщин по числу рождённых детей и др. демографич. факторы рождаемости. Построение комбинир. таблиц рождаемости с учетом брачности и очерёдности рождений позволяет учесть влияние указанных факторов. Путём модификации М. в. н. можно учесть влияние этих факторов и на динамику нас. При этом предпочтение отдаётся дискретной М. в.н., где такая модификация не связана с качеств. усложнением исходной модели.

Методы демографических исследовании, М., 1969, с. 10-47; Паевский В. В., Вопросы демографической и медицинской статистики, М., 1970, с. 100-110; Боярский А. Я., Население и методы его изучения, М., 1975; Демографические модели. М., 1977; Lotka A., Theorie analytique des associations biologiques, P., 1939, Соale A., Demenу Р.,. Regional model life tables and stable population, Princeton [1966]; Concept de la population stable. ONU, N. Y., 1966; Кеуfitz N., F1iegеr W., World population. An analysis of vital data Chi.- L., 1968; Kuczynski R., The measurement of population growth, N. Y.- L.- P., 1969.

Е. М. Андреев.