СИЛА СМЕРТНОСТИ

СИЛА СМЕРТНОСТИ, демографич. показатель, характеризующий меру интенсивности смертности на малом интервале возраста. С. с. равна приведённой к одному году вероятности смерти в течение бесконечно малого возрастного интервала

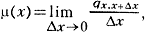
где μ(x) - сила смертности в возрасте х лет, q_x,x+Δx - вероятность смерти в интервале возраста от х до (х + Δх) лет. При этом предполагается, что вероятность смерти в интервале возраста от х до (х + Δх) лет с точностью до бесконечно малой высшего порядка равна произведению С. с. на длину возрастного интервала Δх.

Понятие 'С. с.' введено в демографич. лит-ру Б. Гомперцем в 1825. Самостоят, раздел матем. демографии связан с попытками найти универсальную матем. формулу для С. с. Первый шаг в этом направлении был сделан Гомперцем (см. Гомперца - Мейкема формула). С. с. используется в непрерывных матем. моделях смертности (см. Модели демографические) гл. обр. при установлении связи между разл. демометрич. функциями. Непосредственно в количеств, демографич. анализе С. с., как правило, не применяется.

В отличие от вероятности смерти, к-рая не превосходит единицы, С. с. может быть любым положит, числом. Число умерших в малом интервале возраста есть изменение в этом интервале функции дожития 1(х), т. е. вероятности для новорождённого достигнуть возраста х лет. Оно с точностью до бесконечно малой от длины интервала равно l(x)*μ(x)*Δx. Это означает, что С. с. есть логарифмическая производная функции дожития:

μ(x) = - l'_x(x)/l(x) = - d/dx*lnl(x).

С. с. можно трактовать и как коэфф. смертности на бесконечно малом интервале возраста.

Особую роль С. с. играет при расчёте показателей смертности от отд. причин смерти. Так, в простейшем случае для двух групп причин смерти, смертность от к-рых предполагается независимой в силу правил сложения вероятностей смерти:

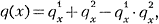
где 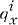- вероятность смерти от i-той причины (i =1,2). Соотношение С. с. существенно проще:

μ(x) = μ¹(x) + μ²(x),

где μⁱ(x) - сила смертности от i-той причины. Это соотношение справедливо при любом числе причин и известно в демографич. лит-ре как закон сложения С. с., сформулированный У. Мейкемом в 1867.

Е. М. Андреев.